Local Search

Strategy: Traverse state space by considering only locally-reachable states

• Start at a random position in a state space.
• Iteratively move from a state to another "better" neighbouring state
• The solution is the final state after a certain number of steps.

Typically, incomplete and **suboptimal

Any-time property: longer runtime, often better solution

• Get a "good enough" solution

Problem formulation in Local Search

Problem formulation is slightly different:

States: Represent different configurations or candidate solution. They may or may not map to an actual problem state, but are used to represent potential solution.

Initial State: The starting configuration (candidate solution)

Note how there are no action/transition properties in the formulation.

Question:

Evaluation Functions

An evaluation function is a mathematical function used to assess the quality of a state.

The function takes in a state as an argument and produces a number.

Important: An evaluation function should only return values between $(negative terminal, positive terminal)$. That is, either terminal state should be more preferrable than any intermediate state.

value = eval(state)

This value can either be minimized or maximized.

• n-queens - number of "safe" queens, we want to maximize
• minimizing a function - minimize the function f(x) itself

Note: a minimization objective f(x) can be transformed into a maximization objective by defining a new objective f'(x) = -f(x) and vice versa

Hill climbing algorithm

current_state = initial_state
while True:
  best_successor = a **highest-eval** successor state of current_state
  if eval(best_succcessor) <= eval(current_state):
    return current_state
  current_state = best_successor

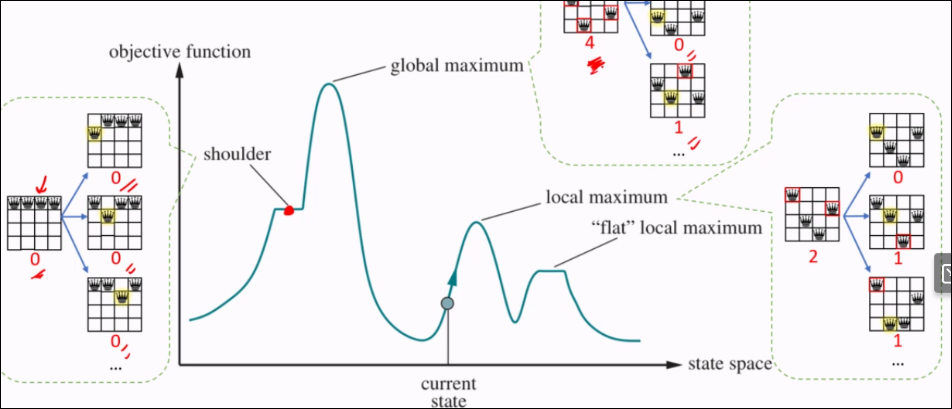
State Space Landscape

• Global Maximum: The overall highest point or solution across the entire state space that represents the optimal solution
• Local Maximum: A point in the state space higher than neighbours.
• Shoulder - A region with a flat area, making it difficult for the algo to move past.

Adversarial Search

Multi-agent problems

A problem that involves multiple agents interacting within an environment, where each has it's own goal(s) and decision-making. Can be cooperative, competitive, mixed-motive.

Competitive Multi-agent problems

Agents have conflicting goals.

Two-player zero-sum games, where one player's gain is another's loss.

Turn-taking games

Next state of environment depends not only on our action in the current turn, but also the other agents in the next turn, which are assumed to be strategic

Designing an agent for competitive multi-agent problems

Game tree

A game tree is a graphical representation of all possible states and moves in a game. Not necessarily a tree.

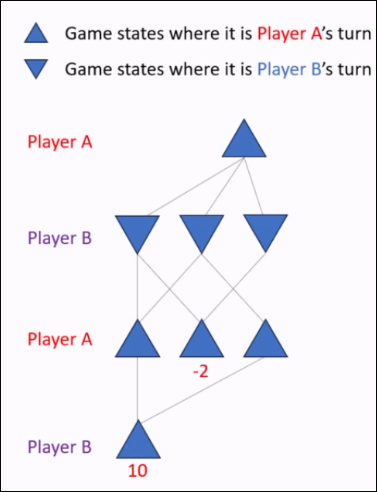
• Nodes indicate all possible game state.
• Edges show legal moves or transitions between states

The outcome of the game is displayed beneath each terminal node (end state).

Problem Formulation

We now have extra properties in the formulation:

• Terminal States: States where the game ends, such as win/lose/draw states. Can be defined as a function.
• Utility Function: Outputs the value of a state from the perspective of our agent.
  • Our agent (player A) wants to maximize the utility.
  • In games such as Chess, outcome is win/loss/draw (+1/0/-1)
  • In games such as Go with territory scoring, outcome for player A is some real number.
  • The utility of non-terminal states is typically not known in advance and must be computed.

Algorithm for Adversarial Search: Minimax

Algorithm specifically for a two player zero-sum game

Core assumption: all players play optimally

Expand function: expand(state)

• For each action, compute: next_state = transition(state, action)
• Returns a set of (action, next_state) pairs

Terminal function: is_terminal(state)

• Returns true/false

Utility function: utility(state)

• Returns a score for the state based on Player A.

def minimax(state):
  (action, v) = max_value(state)
  return action

def max_value(state):
  if is_terminal(state): return utility(state)
  v = neg_inf
  for next_state in expand(state):
    v = max(v, minimum value for player A in the next_state)
  return v

As we can see, the max_value assumes that the opponent plays optimally by minimizing player A in the max_value function.

def min_value(state):
  if (is_terminal(state)): return utility(state)
  v = pos_inf
  for next_state in expand(state):
    v = min(v, max_value(next_state))
  return v

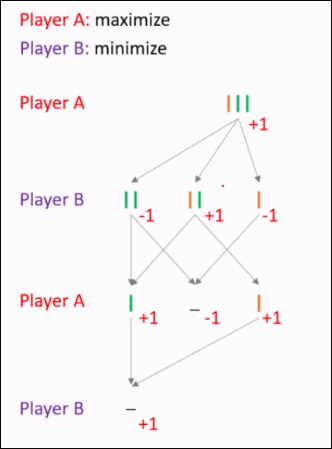So what actually happens in this algo is a step-by-step recursive dive to maximize the minima of a potential branch.

Analysis

Time complexity: Exponential w.r.t. to depth. $O(b^m)$, where b = branching factor & m = max-depth

Space Complexity: Polynomial.

Complete: Yes, if tree is finite.

Optimal: Yes, against optimal opponent.

Optimality

Theorem: In any finite, two-player zero-sum game of perfect information, the minimax algorithm computes the optimal strategy for both players, guaranteeing the best achievable outcome for each, assuming both play optimally

Theorem: If Player A's opponent deviates from optimal play, then for any action taken by Player A, the utility obtained by Player A is never less than the utility they would obtain against an optimal opponent.

The problem with Minimax

Minimax explores the entire game tree.

However, evaluating a node sometimes becomes unnecessary, as it won't alter the decision.

Alpha-Beta Pruning

A variant of minimax that seeks to decrease the number of nodes that are evaluated.

Maintain the best outcomes so far for Player A and Player B:

• Alpha is the highest outcome for player A so far.
• Beta is the lowest outcome for player A so far.

Prune unnecessary nodes.

• At the turn of Player B, if an action leads to a worse outcome for player A, then the rest of the actions are irrelevant; the node will have at most that "worst outcome"
• At the turn of Player A, if an action leads to a better outcome for player A (higher than beta), then the rest of the actions are irrelevant; the node will have at least that outcome which player B is not interested in

Psuedocode

def alpha_beta_search(state):
  (action, v) = max_value(state, -inf (alpha), inf (beta))
  return action

def max_value(state, alpha, beta):
  if (is_terminal(state)): return utility(state)
  v = -inf
  for next_state in expand(state):
    v = max(v, min_value(next_staet, alpha, beta))
    alpha = max(alpha, v)
    if (v >= beta): return v
  return v

def min_value(state, alpha, beta):
  if (is_terminal(state)): return utility(state)
  v = inf
  for next_state in expand(state):
    v = min(v, max_value(next_state, alpha, beta))
    beta = min(beta, v)
    if (v <= alpha): return v
  return v

Alpha-Beta Pruning analysis

Theorem: Alpha-beta pruning does not alter the minimax value, and the optimal move computed for the root node; it only reduces the number of nodes evaluated.

Making full use of alpha-beta pruning requires meta-reasoning: reasoning about which computations to do first (e.g. which branch to expand to first?)

Theorem: Good move ordering increases alpha-beta pruning effectiveness; with "perfect ordering", its complexity is $O(b^{\frac{m}{2}})$

Imperfect Decisions by Using Cutoff on top of Alpha-Beta

Instead of evaluating full tree,

• Cutoff strategy - halt search in middle & estimate value using evaluation function.

Modification: simply start returning an eval function at cutoff:

Evaluation Function

Assigns score to a game state, indicating favourability to a player.

• If terminal state, use utlility(state)
• If not, use a heuristic

Heuristic function is an estimate of utility

• A heuristic should fall somewhere between the minimum and maximum utility for all states.
• Computation must not be too expensive
• In adversarial search, admissibility and consistency properties do not apply

Inventing a heuristic

• Relaxed game - in principle, but usually too costly
  • Chess, each peice can teleport/self-sacrifice
• Expert Knowledge
  • Often use features like material count, mobility, safety
• Learn from data
  • Heuristic function could be learned from labeled dataset.

Optimality

Theorem: In a finite, two-player, zero-sum game, the minimax algorithm with cutoff and an evaluation function returns a move that is optimal with respect to the evaluation function at the cutoff

The move may be suboptimal with respect to the true minimax value